What Happens in Math Class
Experiments with math at our microschool
“To trick her mother into thinking she walked up 13 floors!”
“Maybe she’s doing more exercise?”
“She wanted her mother to think she actually did exercise.”
“Well, not to trick her mother but to show her.”
These are some of the reasons the kids came up with in response to the puzzle. These lines don't capture the richness of how the kids explore the problem—how their minds and bodies (yes, bodies) are at work. How there is some form of learning happening at all times. Here’s an unfiltered glimpse.
What they are doing is thinking through this puzzle in Math Lab (what we call math class at Comini, so we can remind ourselves that exploration and experimentation are at the heart of it).
I often struggle to explain what we do with math at Comini. It quickly becomes an impassioned recital of what we don't do (rote memorization, jargon without reason, etc.) and broad terms for what we do and why. And that is playful exploration. because learning is trekking through a rich landscape of possibilities. That’s a vivid and enormously useful metaphor we derive a lot from (link to a much longer article on learning as exploration). But what does that exploration mean in the context of something like math?
This is what it looks like.
It is exploring possibilities, flopping around while thinking, running off to play the guitar, wandering from the problem at hand to the possibilities of the day and back.
I give them a hint. "Focus on the first line." I read it with emphasis. They all focus on the word "shy" with renewed excitement.
"Ah, she didn't want to meet someone on the 8th floor!"
"She wanted to avoid meeting someone in the lift."
Not bad, but this is a puzzle and that isn't the answer. I ask them to read the first line again.
We do everything possible to take the mystery out of math. It's often all drills and monotonous manipulation without meaning and magic.
Math is the language of precision, patterns, and possibilities. We use math to go from "kind of this big" to "exactly this much," from "once in a blue moon" to "every 12 years." Yes, there is poetry, but it's the immense practicality—which is all around us in the modern world—that makes it so powerful.
But, for some bizarre reason, math is also the only language where we attempt to teach its script before learning to speak it! 1, 2, 3, and 0 are not math. They are symbols we use as shorthand for mathematical concepts.
Unlike any other language, which can be picked up by simply being immersed in it, math requires us to pay attention to things, even defocus from what we normally see and "look" at what is hidden. That isn't just a bunch of tomatoes—it is also, if you look closely, three distinct things. And there is something profound and universal about that three-ness. We can see it, imagine it, associate it with any object in the universe and create an utterly different picture of three things, which is nothing like our bunch of tomatoes, but still has that three-ness.
That makes it a tricky language to learn by mere immersion. It helps to have a guide directing our attention to certain aspects, making us look again when we think we've seen and recognized it all. As Piaget told us, and neuroscience repeatedly reminds us, children normally go from exploring and internalizing the concrete to imagining the abstract. They must learn to navigate their world in the present before exploring the realm of possibilities.
Our math guidance should keep that in mind. Here are our guidelines for how to do it, with a natural order to follow. What should we do initially, and how do we expand on it? We know we have a great math activity when it meets all these criteria.
Feel It First
It makes sense when we can connect it to our world. At an early age, that quite literally means holding things, feeling them, allowing our minds and bodies to internalize their forms—while also grasping the concept of discreteness and counting, without necessarily knowing those words. Montessori schools emphasize number rods, but nearly anything in our modern world of abundance will do. We use pebbles to get kids started with the idea of counting and numbers. Feeling it also means grounding it in their world. Eva's world is one they can imagine and almost feel their way through. They can picture her running down to Joggers' Park and taking the metallic mirrored elevator back. It isn't some dry word problem asking them to count petals on a worksheet flower.
Make It Matter
Our conventional math curriculum almost looks like its only use is in creating artificial problems for meaningless exams to get into college. Math is profoundly useful and exists everywhere in our lives and in our kids' lives. Let them see it, realize it, and understand how it helps. In this case, numbers aren't used directly, but sizes and dimensions are (puzzle hint!).
Play With Ideas
The answer isn't the important thing here. It's how kids explore the conceptual space. What are the logical clues here? Is it Eva's attempt to convey something beyond the literal, or is it something in her character that narrows the space of possibilities? In exploring these, kids unpack mathematical reasoning. They learn to distill the rich picture of life into essential ideas and move them around to arrive at something new.
Literal play helps here as well. We love using board games and making board games that allow us to do this. Classics like Catan help drive home how being able to quantify and track resources can help, and to gradually build up ideas about optimizing their judicious use to achieve outcomes. Math becomes the indirect means to having fun.

Ask Why Before How
In a typical classroom setting we are asked to dive into mathematical manipulations without asking why. "Because it is part of the curriculum" is the implicit answer that is universally rejected by young minds. The why should matter, and connect to their world. Why should I care about adding numbers? Or multiplying them? Why does Eva stop at floor 7, and not floor 6 or 8? Why does that number matter?
Stay With It
The usual focus on efficiency is counterproductive. Your wrist-watch is now capable of faster calculations than you will ever be. It is 2024 and we don't need to be computers or calculators. What matters is how we translate the problem at hand into a mathematical perspective. This often takes time and exploration. And that can be fun! Allow them to wallow and wander for the wonder to emerge. Why did Eva choose that floor? What other reasons might she have had? How many possibilities can we discover? What patterns emerge?
See It Everywhere
Every aspect of our modern world can be heard in the language of math. We can count seasons, stars, time, calories, social media clicks, and quantum bits. It is in the tiniest things and the most unimaginably vast things. By limiting math to dry problems in textbooks we are limiting imagination. Assigning mathematical ideas to the real world helps us in many ways. Why do we number floors and count minutes? We should be able to ask why and try to find our own answers before being given them.
The Map Is Not the World
To facilitate math in this playful exploratory way doesn't mean we can't have a plan. The mathematical landscape has been charted out and we have maps we can use. And we do, in fact, use such personalized maps to understand where exactly each child is on this landscape.
But, as educators everywhere realize, maps can make us focus too narrowly and lose sight of the bigger picture. This is exactly what happens in conventional classrooms across the world when the commonly used map—the curriculum—becomes the sole focus. It becomes so because we evaluate children based on their ability to remember the map. We set out with the noble goal of creating explorers, but end up with map memorizers because we teach to the test.
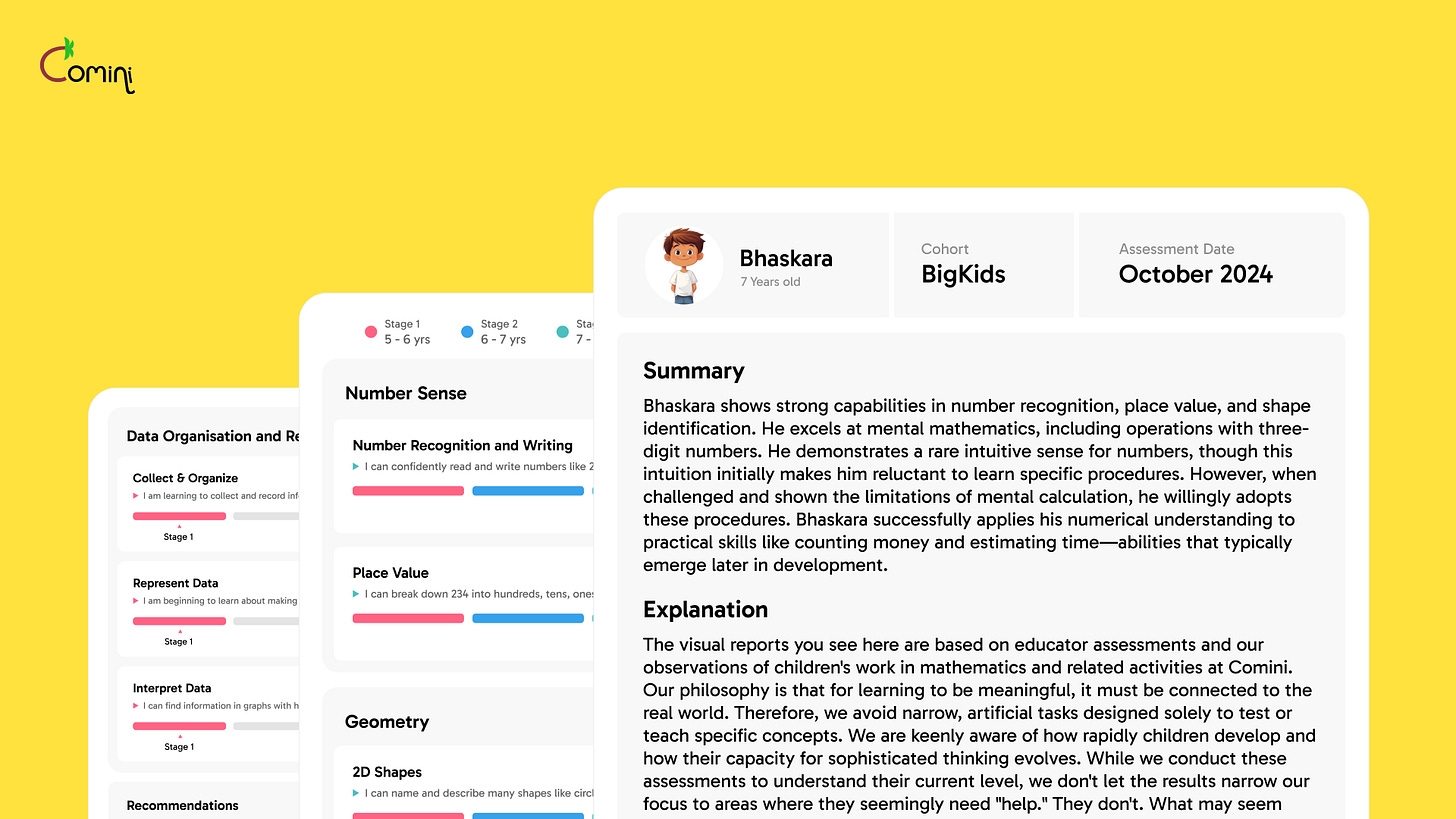
We use maps as a handy reference while firmly believing there's no such thing as needing to know something by a certain age (an unfortunate belief that leads to math phobia for so many).
The numbers in the puzzle don't merely serve the needs of a narrow curriculum but reference the richness of the world they inhabit. Floor numbers in the elevator do not just map to the specific floor, but also have a spatial relationship that is maintained in how they are laid out. (Another puzzle hint!)
Alternative approaches to learning math aren't new. We are rediscovering what many others across the world have explored over the last few decades. Just to name one example, here is a brilliant book by a Russian mathematician recounting his explorations of math with a group of preschoolers in the 1980s. Why hasn't this playful approach become more widespread? Before the internet, one needed specialized resources to look up interesting approaches to specific concepts, to understand how to answer the many whys kids could ask. YouTube has made that exploration trivially easy. Now it requires only a willingness to learn anew, to explore with fresh eyes, and to ask the right questions. Asking the right questions remains challenging for many adults—we were never encouraged to ask why, only to master the how. Adults could use a helping hand to learn how to ask and learn, so they can pass insights along early. We believe this and the coming generation of AI tools are going to make this possible. We use AI to facilitate many aspects of learning and are building copilots to help adults (parents and educators) become more effective facilitators.
I ask them to read out the first line again. Nico eventually gets it! Their faces light up. What a delightful moment that is, when the pieces click together in place and the resonant picture emerges.





This was a brilliant read. (And, I still haven't solved the puzzle.)